Seguridad, criptografía y grupos simétricos

Hoy en mi clase de matemática discreta hablamos sobre criptosistemas, y en especial, sobre el sistema RSA como un ejemplo de un sistema de llave pública.

Un ejemplo de un criptosistema sencillo es cuando en la escuela jugábamos a mandar mensajes o hablar un lenguaje inventado, el cual solo uno y su mejor amigo sabían hablar. Para esto, se tiene una llave que sirve para encriptar el mensaje,  y la misma llave sirve para descifrarlo. Esto puede ser muy sencillo de implementar, sin embargo cuenta con la desventaja de que debe haber una reunión previa para ponerse de acuerdo en la llave, es decir el cifrado. 

En el ámbito de la escuela, esto resulta suficiente, sin embargo para aplicaciones mas elaboradas, como transacciones por internet, resulta poco práctico. Si por ejemplo compro algo por internet, quiero enviar me manera segura mi numero de tarjeta de crédito, es decir, que solo el destinatario pueda leerla. Siguiendo el sistema anterior, para poder enviar mi mensaje, tendría que haberme reunido con el vendedor anteriormente y ponerme de acuerdo con el en una clave, pero si me hubiese reunido con el antes, le hubiera dado mi número de tarjeta en primera instancia y no me encontraría en este dilema.

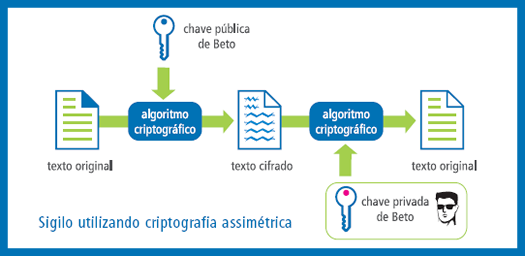
La idea de los criptosistemas modernos (asimétricos) es prescindir de la necesidad de un acuerdo previo, y hacerlo todo remotamente. Suena como magia negra, y en cierto modo, lo es.

La magia negra utilizada es matemática, y en particular, algebra moderna. La idea es poder crear una forma de cifrar y descifrar mensajes que resulte difícil de hackear.  Ahora bien, el problema comienza con entender qué significa que algo sea difícil de hackear.

Primero, nuestro objetivo es poder mandar mensajes de una forma segura a través de un canal inseguro. Para esto tenemos un conjunto $M$ de mensajes que podemos mandar. Antes de cifrar un mensaje, es necesario codificarlo, lo que significa traducir la información y manejarla como un objeto matemático.

Para codificar un mensaje, tenemos un conjunto $G$ de códigos y una función codificadora

$$g:M\to G\,,$$

$$m\mapsto g(m)\in G\,.$$

Esto simplemente es una traducción y no contiene ningún aspecto de criptografía, al menos no algo relevante.

Luego, tenemos una función encriptadora,

$$E:G\to G\,,$$

la cual sirve para cifrar los mensajes. Nótese que no se tratan de los mensajes en si, sino de la codificación de los mismos.

Por último, se tiene una función desencriptadora,

$$D:G\to G\,,$$

tal que $D\circ E=\text{Id}$, la identidad en $G$. Con esto,  el proceso total para transmitir un mensaje $m$ resulta ser

$$g^{-1}\circ D \circ E\circ g(m)=m\,.$$

La parte relacionada con criptosistemas se enfoca en el medio, en $E$ y $D$, la cual es mas teórica. La parte de codificación tiene que ver mas con aspectos físicos del medio sobre el cual se realiza la transmisión.

Ahora bien, la magia de la criptografía recae en el conjunto $G$ y las funciones definidas sobre $G$. Desde un punto de vista computacional, $E$ y $D$ son algoritmos que poseen cierta complejidad computacional. Que nuestro sistema sea difícil de hackear significa que las funciones sean altamente complejas. Esto, a grandes rasgos, significa que es necesario invertir muchos recursos para poder obtener un resultado. Generalmente el recurso crítico resulta ser el tiempo.

Las funciones $E$ y $D$ son las que se conocen como las llaves del criptosistema, y es necesario entonces poder tener una forma de generar dichas llaves.

Una de las maneras de atacar esto es hacer que el conjunto $G$ tenga la estructura de grupo. Entonces, se pueden ver a las llaves como pertenecientes al conjunto de biyecciones de $G$ en si mismo, es decir, permutaciones.

Para efectos prácticos, $G$ es un grupo finito, digamos con cardinalidad $n$. Entonces se tiene que las posibles llaves son elementos del grupo de permutaciones $S_n$, el cual tiene $n!$ elementos.

Puesto que una llave $A$ es un elementos del grupo $S_n$, sabemos que su inverso $A^{-1}$ es otro elemento de $S_n$, es decir, es otra llave.  Por lo tanto $(A,A^{-1})$ sirven para encriptar y desencriptar mensajes, y vice versa.

La idea con sistemas de llave pública es que se hacen públicos el grupo $G$ y la función $A$ y se mantiene la función $A^{-1}$ en secreto. La magia del asunto es que nada más teniendo $G$ y $A$, calcular $A^{-1}$ resulta ser difícil computacionalmente hablando. Sin embargo, teniendo toda la información, sobre $G$, es fácil generar $A$ y $A^{-1}$.

Generalmente la generación de pares de llaves se realiza en base a parámetros aleatorios. Esto es, la llave $A$ depende de parámetros que uno puede escoger, es decir,  $A(P)$. Conociendo estos parámetros, es fácil generar $A^{-1}(P)$, sin embargo, sin los parámetros $P$, esto resulta difícil.

Al no tener los parámetros $P$, alguien puede encontrar $A^{-1}$ nada mas por prueba y error, tratando de encontrar el inverso de $A$ en $S_n$, multiplicando $A$ con cada elemento hasta encontrar la identidad. Para valores pequeños de $n$ esto resulta no ser tan tedioso, sin embargo ya para $n=60$ tenemos que $S_n$ tiene más elementos que el número de átomos en el universo visible.

Al final, lo crucial es el algoritmo $A(P)$, el cual toma parámetros y devuelve un elemento de $S_n$, es decir

$$A:\mathcal{P}\to S_n\,,$$

donde $\mathcal{P}$ es el espacio de parámetros, el cual suele ser un producto cartesiano del tipo $\mathbb{F}^k$.

Por lo tanto, se puede decir que el cuadro completo es

$$g^{-1}\circ A^{-1}(P)\circ A(P)\circ g(m)\,,$$

Cuando $G=\mathbb{Z}_{pq}$ tenemos el caso de encriptación RSA. Al considerar $G$ como puntos en una curva elíptica, se obtiene la criptografia de curva elíptica, y así con cualquier grupo $G$.

Siguiendo la misma idea, es posible considerar criptografía con matrices, nudos, simetrías, cohomologías y cualquier grupo que se pueda imaginar. Acá hay una lista de grupos no tradicionales con los cuales sería posible realizar criptosistemas.