Hace unos días veíamos propiedades de convergencia de series en mi clase de cálculo dos y algunos alumnos comenzaron a preguntar y mencionar sobre series divergentes. Hay un par de videos famosos sobre $$\sum_{n=1}^\infty (-1)^n=\frac{1}{2}$$ y $$\sum_{n=1}^\infty n=-\frac{1}{12}$$.
Al pensar sobre estas, se me estaba ocurriendo que tipo de regularizaciones pudieran hacerse codificando ritmos musicales como series infinitas.
Por ejemplo, el ritmo de rock and roll clásico puede realizarse con bombos en los tiempos 1 y 3 y caja en los tiempos 2 y 4.
Si codificamos un golpe de caja con un +1 y un golpe de bombo con -1, tendríamos que el ritmo de rock and roll estaría dado por
$$1-1+1-1+1-1+1-1+\dots$$
Esta serie se conoce como la serie de Grandi y es una serie divergente. Sin embargo, es posible regularizarla y otorgarle un valor numérico,
$$\sum_{n=0}^\infty(-1)^n=\frac{1}{2}\,.$$
Ahora bien, regularizar una serie no significa que la serie sea igual a dicho valor, sino que significa que es posible hacerle corresponder un valor real a la serie de tal manera que ciertas propiedades de series sean satisfechas.
La mayoría de las regularizaciones de series vienen dadas dentro de un contexto físico, y en nuestro caso, de un patrón rítmico. El resultado asignado de $1/2$ puede interpretarse como que del total del ritmo, la mitad del tiempo se toca la caja y la otra mitad se toca el bombo.
Si por ejemplo vemos otro ritmo como el vals, este se representa en 3 tiempos, donde el 1 es el bombo y la caja se toca en el 2 y 3. Con nuestra codificación, el ritmo de vals se representa por medio de la serie
$$-1+1+1-1+1+1-1+1+1-1+1+1-\dots$$
Esta serie, al igual que la anterior diverge, pero al contrario de la primera, no es una serie tan famosa, por lo que es necesario trabajarla un poco para poder encontrar su valor de regularización.
Usualmente, el truco para regularizar una serie
$$\sum_{n=0}^\infty a_n$$
es agarrarla sucesión $\{a_n\}$ y construir una función analítica $f(x)$ basada en la sucesión. Luego se busca una representación en forma cerrada de $f(x)$ y se reemplaza el valor de $x$ que regularice la suma. Usualmente es común analizar funciones generatrices del tipo
$$f(x)=\sum_{n=0}^\infty a_nx^n\,,$$
o bien, funciones L (funciones zeta) del tipo
$$g(s)=\sum_{n=0}^\infty a_nn^s\,.$$
En este caso, nuestra sucesión está dada por $$a_{n+1}=1-a_{n}-a_{n-1}, \qquad a_0=-1, a_1=1$$
Cuya solución general está dada por $$a_n=\frac{1}{3}\left(1-4\cos(2\pi n/3)\right)\,.$$
Teniendo el término general de la sucesión, es posible obtener la continuación analítica de $g(s)$, y nuestro valor deseado ocurre para $s=0$,
$$g(0)=-\frac{5}{6}$$.
Por ejemplo, para otros ritmos
$$
\newcommand\T{\Rule{0pt}{1em}{.3em}}\begin{array}{l|c|c}
\text{Ritmo} & \text{patrón} & \text{valor de la serie}\\
\hline
\text{Blues} & -1+0+0+1+0+0 & -\frac{1}{2}\\
\hline
\text{Funk} & -1+0+1-1+0-1+1+0 & -\frac{7}{8}\\
\hline
\text{DnB} & -1+0+1+0+0-1+1+0 & -\frac{3}{8}\\
\hline
\end{array}$$
donde -1 representa el bombo, +1 la caja y 0 un tiempo no acentuado.
Friday, December 12, 2014
Monday, September 1, 2014
Lights out and Matrices over Z_2
A couple days ago, one of my friends challenged me to solve a riddle posted by spanish newspaper El País. The riddle consisted in explaining why in a 24x24 board, there are impossible configurations of the game Lights Out (you can play it here)
It had two parts:
- the first one was to find an impossible configuration, that is, a configuration of lit squares on the board that was impossible to reach starting from a dark board (equivalently, a starting configuration for which you can't turn the lights out).
- the second was to show that at least half of the possible configurations on the board are impossible.
The first part requires a bit of trial and error, but one can find it. The second part obviously implies the first, and also is more interesting.
One trick to attack the problem is to think about it in the general case, on a $n\times n$ board. You quickly realize that the $1\times 1$, $2\times 2$, and $3\times 3$ have no impossible configurations, that is, you can reach any configuration starting from a dark board.
Why is 24 so special then? First of all, notice that since the squares only have two states (on or off), the only thing that determines the state of a square is the parity of the number of times that it has been pushed. More over, we can reduce this to either 0 or 1.
Checking the above set up, one can see that pressing the squares with 1's, we end up with a dark board when $n=4$. Hence, there are two different pushing patterns (this and all 0's) which lead to a dark board. This means that every possible configuration of lights can be achieve at least twice with different pushing patterns (adding the above pushing pattern to any other will make to end up with the same light configuration).
Thus the $4\times 4$ case is the first one to have impossible configurations, and actually, at most half of the possible light configurations are possible.
It is not difficult to see that this pattern can be used to treat bigger boards.
For example, the above configuration with lead to a dark $9\times 9$ board. In general, this is possible for $n=5k+4$. Therefore $n=24$ will have the same behavior.
Now, this whole thing smells a lot like linear transformations of vector spaces. And indeed, a nice way to attack the problem is using this language.
Let $p=(p_1,p_2,\dots, p_{n\times n})$ (yes, $n\times n$) be the vector of pushing parity for an $n\times n$ board, were we read the pattern right to left, top to bottom. Thus the dark pushing pattern for the $4\times 4$ is
$$p=(0,1,1,0,1,0,0,1,1,0,0,1,0,1,1,0).$$
Let $A$ be the $n^2 \times n^2$ matrix that gives the light configuration obtained by the $p$ pushing pattern, i.e. $(Ap)^T$ is a vector giving the state of a square (on or off). We use the same convention for reading out this vector.
Hence, a number $n$ will lead to impossible configurations if and only if $A$ is non-invertible. To be more rigorous, we have the following:
$V$ is the vector space $(\mathbb{Z}_2)^{n^2}$ with $\mod 2$ addition, and $A$ is the matrix from $V$ to $V$ containing the rules of the game.
This matrix can be written in block form as the symmetric tridiagonal matrix
$$A=\begin{pmatrix}B & I_n & 0 & \cdots & 0\\ I_n & B & I_n & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & B\end{pmatrix}$$
with $I_n$ the $n\times n$ identity matrix and $B=I_n+U_n+L_n$, where $L_n,U_n$ are the lower and upper shift matrices.
Therefore, there are impossible configurations if and only if $\det (A)=0$. Since $B, I_n$ commute with each other, we can calculate the determinant in block form.
Here is a list of the first few determinants
n
|
det(A) (block polynomial)
|
det (A)
|
1
|
I
|
1
|
2
|
B^2 – I
|
-3=1
|
3
|
B^3 - 2*B
|
-7=1
|
4
|
B^4 - 3*B^2 + I
|
0
|
5
|
B^5 - 4*B^3 +
3*B
|
0
|
6
|
B^6 - 5*B^4 + 6*B^2 – I
|
2197=1
|
7
|
B^7 - 6*B^5 +
10*B^3 - 4*B
|
-34391=1
|
8
|
B^8 - 7*B^6 + 15*B^4 - 10*B^2 + I
|
-4002939=1
|
9
|
B^9 - 8*B^7 + 21*B^5
- 20*B^3 + 5*B
|
0
|
Notice that the coefficients of the block polynomials are Pascal's triangle's.
Hence, we can see that (as expected) $n=9$ gives impossible configurations, however the unexpected $n=5$ appears, so another set of values for $n$ will lead to impossible configurations $n=6k+5$.
A good question would be to find all such possible $n$ leading to impossible configurations, but that might be a task for another time.
Lastly, in order to solve the game for any of the possible $n$'s, the only thing needed is to compute $A^{-1}$ and apply it to the configuration, obtaining the pushing pattern.
Monday, August 18, 2014
El tráfico: caos, fractales y fluídos.
El tráfico siempre me hace pensar. A veces cosas buenas, cuando voy en carretera, y a veces no tan buenas cuando hay un carro atravesado en un semáforo.
Siempre me ha parecido un tema interesante de analizar, y por supuesto, de querer modelar. Modelar algo significa entenderlo, analizarlo, pensar como piensa el fenómeno. Como dijo Richard Feymann, "lo que no puedo crear, no lo entiendo".
Entender el tráfico es una tarea muy difícil, pues intervienen muchos factores tanto físicos como psicológicos, al final de cuentas son seres humanos los que conducen (por el momento).
El tráfico es caótico. Y no solo por como coloquialmente le decimos, sino que también es matemáticamente caótico. En pocas palabras, un sistema es caótico si pequeños cambios iniciales desencadenan grandes cambios posteriores. En algunas ciudades esto se logra apreciar desde el diseño mismo de las vías, en donde un cruce incorrecto a la derecha, le puede hacer perder a uno hasta media hora.
Así mismo, al tomar al tiempo como variable, muchas veces se tiene un sistema caótico. A veces salir 5 minutos más temprano es la diferencia de llegar una hora tarde o no a algún lugar.
Tanto espacialmente, como temporalmente, el tráfico es un sistema caótico, por lo que patrones fractales comienzan a emerger. Se puede analizar el tráfico considerando principalmente dos funciones
$$f:\mathbb{R}^2\to\mathbb{R}^+$$
$$g:\mathbb{R}^+\to\mathbb{R}^+,$$
donde $f$ mide cuando se tarda en llegar a un lugar dado dependiendo de la posición de salida, y $g$ mide cuanto se tarda en llegar a un lugar dado dependiendo de la hora de salida de un lugar fijo.
En estos dos casos simples, $f$ y $g$ son sensibles a grandes cambios debido a pequeñas perturbaciones en el dominio.
Otra manera de analizar el tráfico es de manera continua, como un flujo. A veces es posible aproximar sistemas discretos por medio de sistemas continuos para simplificar el análisis.
Por ejemplo, ¿qué pasa si una parte de la carretera se reduce de dos a un carril? Desde el punto de vista de un. flujo, se puede obtener una aproximación del tráfico utilizando la ecuación de continuidad:
$$2V_1=V_2$$
y el tráfico irá a la mitad de la velocidad en la sección de dos carriles. ¿Qué pasaría si se aumentan a 4 los carriles de la primera sección? Ahora se tendría que la velocidad $V_1'$ es 4 veces más lenta que $V_2$. Pero ¿cómo se compara el tiempo de recorrido en estos escenarios?
Supongamos que el trayecto total mide 1 y que el cambio de numero de carriles pasa en 1/2. Entonces con solo un carril, el trayecto duraría
$$t=\frac{1}{V_2},$$
con el cambio de 2 a 1 carril, el tiempo total es de
$$\frac{1/2}{V_1}+\frac{1/2}{V_2}=\frac{1}{V_2}+\frac{1}{2V_2}=\frac{3}{2}t,$$
y con el cambio de 4 a 1
$$\frac{1/2}{V_1'}+\frac{1/2}{V_2}=\frac{2}{V_2}+\frac{1}{2V_2}=\frac{5}{2}t.$$
Esto significa que entre más carriles una conexión tenga, si la velocidad en la sección 2 es constante, más tardado es el trayecto total. Para aumentar la velocidad del flujo vehicular, se debe aumentar la velocidad de las salidas y disminuir el número de carriles.
Un análisis mas completo del flujo del tráfico se logra por medio de la ecuación de Burgers. Acá se modela al tráfico como un flujo incompresible. Con esta ecuación se toma la interacción entre vehículos, es decir, el factor psicológico entre los conductores. Una causante del tráfico es la reacción en cadena que los conductores realizan al frenar. Es el mismo efecto que se observa cuando un semáforo marca a verde. Hay un desfase entre el cambio del semáforo y comenzar a andar en el carro. Esto es debido al tiempo de reacción de los conductores y los que lo preceden en la cola.
De igual manera ocurre cuando se frena en la carretera, los conductores que vienen detrás experimentan ese mismo tipo de reacción, similar al de un fluido viscoso. Es por eso que la ecuación de Burgers representa una manera eficiente de modelar el flujo del tráfico.
¡Se pueden pensar cosas interesantes en el tráfico!
Sunday, July 20, 2014
The Monty Hall Problem, a problem of common sense
A few days ago, my friend Javier posted something about the Monty Hall Problem on Facebook. This is a well known riddle in which the use of probabilities saves the day.
In this conundrum, we are to choose one out of three doors to win a prize. Typically, the prizes are taken to be a car and two goats. After making the decision, the game host opens a door (showing a goat) and asks you if you want to switch or stay with your initial door.
Naively we can think that after the host shows one of the three doors, there is a 50% chance to win the car with the remaining two doors, so one might think that it does not make any difference to change door or not.
With a more detailed analysis (e.g. in the video) one can see that changing door is the best option. This is generally achieved using probabilities, but actually, switching doors is the most common sense thing to do.
It all relies on the concept of information.When we choose the first door, we don't have any information over the distribution of the prizes. After the host opens one of the doors, we do have information concerning this distribution. Not making any action would imply that we are neglecting that information, or in other words, wasting that information.
One realization of information is that it clarifies the uncertainty of a system. That is, first we were completely uncertain of the distribution of the prizes. Then, when the host opens a door, that uncertainty is reduced, as we know something about it. Hence, not performing any action is not taking advantage of this fact.
This is an example of Shannon's entropy. In some sense, entropy is the measure of uncertainty or disorder of a system. In this case, the system is the distribution of the prizes behind the doors. When one of the doors is revealed, the entropy decreases. Using the analogy with thermodynamics, entropy measures the quantity of energy that becomes useless to do work. Hence, decreasing the entropy means that there is more energy that potentially can be used to do work.
Similarly, in information theory, we can think of a decrease of Shannon's entropy as a way to potentially do something in the system, to make use of that information and utilize it for a goal. Not making any action in our Monty Hall Problem means that we are wasting resources and not taking the opportunity of using this potential ability of doing a something.
Changing doors is the most common sense thing to do, as naively, we can think that knowledge is power and that extra knowledge is the ability of doing something.
Similarly, data or statistical information without any reaction is a complete waste of resources. Having data or statistics and not doing anything with it besides displaying, it is like having no information at all. In fact, is much worse, as you let go the opportunity of doing something with that information.
Sunday, January 19, 2014
Amistad y geometría hiperbólica
Hace unos días, un amigo publicó en Facebook que uno es el promedio de las cinco personas con las que más se relaciona. Me llamó la atención por varias razones. Primero, porque me dio curiosidad saber en qué medían a las personas para poder hacer el promedio (cosa en la que no voy a profundizar), y segundo, porque me recordó a un viejo problema de olimpiadas
Consideremos un retículo entero indexado por el conjunto ZxZ (por ejemplo, el conjunto de puntos
de coordenadas (m, n), con $m, n \in Z$). En los vértices de este retículo ponemos enteros positivos
de acuerdo a la siguiente regla: el número correspondiente a un vértice es el
promedio de los números colocados en los vértices vecinos (Cada vértice tiene cuatro vecinos
correspondientes a los cuatro puntos cardinales, por ejemplo: los vecinos de (3, 5) son
(3, 4), (4, 5), (3, 6), y (2, 5). Así que si los números colocados en (3, 4), (4, 5), (3, 6), y (2, 5),
son 2, 4, 1, 1, respectivamente, entonces el número colocado en (3, 5) es $\frac{2+4+1+1}{4}=2$ ).
Demostrar que todos los números colocados en el retículo deben ser iguales.
En espíritu, estos dos problemas son muy parecidos, y por eso me llamó mucho la atención, puesto que la única solución al problema del promedio de las cinco personas, de acuerdo al problema anterior, es que todas las personas son iguales. La diferencia es que el problema de olimpiadas asume que se trabaja con enteros, y aún mas, con todos los enteros. El problema de las personas es definitivamente finito, y por lo tanto la conclusión de uniformidad no es válida.
Por lo tanto, me llamó la atención como pudiera caracterizarse este problema. Siguiendo la misma idea del problema olímpico, asignemosle a cada persona un par ordenado $(x,y)$ en el plano cartesiano. Sea $f$ la funcionó del plano que le asigna su medición de acuerdo a alguna regla (la medición de la que pueda hablar el articulo).
La condición dada en el articulo es entonces que cada persona debe ser el promedio de sus cinco vecinos mas próximos, es decir, cada persona es el baricentro del pentágono formado por sus cinco amigos más cercanos.
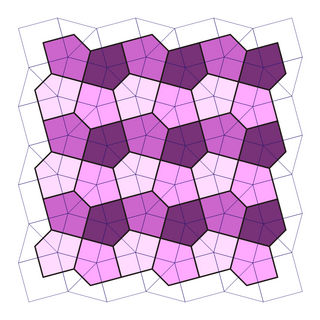
Al pensar el problema de una manera un poco más geométrica, pudiéramos pensar entonces que este problema se traduce a teselaciones utilizando pentágonos.
Consideremos un retículo entero indexado por el conjunto ZxZ (por ejemplo, el conjunto de puntos
de coordenadas (m, n), con $m, n \in Z$). En los vértices de este retículo ponemos enteros positivos
de acuerdo a la siguiente regla: el número correspondiente a un vértice es el
promedio de los números colocados en los vértices vecinos (Cada vértice tiene cuatro vecinos
correspondientes a los cuatro puntos cardinales, por ejemplo: los vecinos de (3, 5) son
(3, 4), (4, 5), (3, 6), y (2, 5). Así que si los números colocados en (3, 4), (4, 5), (3, 6), y (2, 5),
son 2, 4, 1, 1, respectivamente, entonces el número colocado en (3, 5) es $\frac{2+4+1+1}{4}=2$ ).
Demostrar que todos los números colocados en el retículo deben ser iguales.
En espíritu, estos dos problemas son muy parecidos, y por eso me llamó mucho la atención, puesto que la única solución al problema del promedio de las cinco personas, de acuerdo al problema anterior, es que todas las personas son iguales. La diferencia es que el problema de olimpiadas asume que se trabaja con enteros, y aún mas, con todos los enteros. El problema de las personas es definitivamente finito, y por lo tanto la conclusión de uniformidad no es válida.
Por lo tanto, me llamó la atención como pudiera caracterizarse este problema. Siguiendo la misma idea del problema olímpico, asignemosle a cada persona un par ordenado $(x,y)$ en el plano cartesiano. Sea $f$ la funcionó del plano que le asigna su medición de acuerdo a alguna regla (la medición de la que pueda hablar el articulo).
La condición dada en el articulo es entonces que cada persona debe ser el promedio de sus cinco vecinos mas próximos, es decir, cada persona es el baricentro del pentágono formado por sus cinco amigos más cercanos.
Al pensar el problema de una manera un poco más geométrica, pudiéramos pensar entonces que este problema se traduce a teselaciones utilizando pentágonos.
Puesto que estamos hablando de un conjunto finito de personas (grande pero finito!), resulta natural pensar que se trata de teselaciones de la esfera.
Al tener una de estas teselaciones de la esfera, la condición del baricentro se vuelve en requerir que $f$ sea lineal en este espacio (los vértices de la teselacion), puesto que una función lineal respeta combinaciones lineales. Esto sería un tema de teoría ergódica.
Regresando al tema, la teselación anterior es conocida como la teselación de El Cairo, compuesta de hexágonos descompuestos en pentágonos. Esta es una teselación dual de la teselación de cuadrados truncados
Una telesación dual es aquella que se obtiene por medio de unir los centros de las fugaras que componen otra teselación. Generalmente las estructuras duales poseen características similares, por lo que sería interesante ver la teselación dual de la relación estudiada en el artículo de los cinco amigos. Acá, la teselación dual la relación entre uno y los amigos de nuestros cinco amigos, en otras palabras mediría la influencia en uno de los amigos de nuestros amigos. De estar trabajando con funciones lineales (ergódicas), tendríamos, como es de esperarse, que somos el promedio de los amigos de nuestros amigos.
Este mismo análisis puede continuarse aumentando los grados de separación obteniendo resultados similares. Nótese que al ir aumentando los grados de separación, la influencia hacia uno mismo va disminuyendo.
Finalmente, al trabajar con un conjunto finito, se tiene que $f$ debe alcanzar un mínimo y un máximo, lo cual contradice que cada punto sea el medio de otros cinco, y daría como conclusión que todos los puntos son iguales, es decir, que $f$ es constante.
De esta manera, para que este resultado sea válgido, tendríamos que hablar de una geometría no Euclideana, muy probablemente de una geometría hiperbólica. De esta manera, nuestro conjunto finito (personas) puede ser dotado de una estructura no acotada, la cual nos haría evitar el resultado que $f$ sea constante.
Subscribe to:
Posts (Atom)