Orbit-Stabilizer and Covering Maps

Last week, in our quantum Mechanics class, we were going over symplectic spaces and symplectic transformations. A symplectic space is just a manifold together with a skew-symmetric non-degenerate bilinear form $J$ defined on it, and a symplectic transformation $S$ is a transformation of the manifold into itself such that it preserves $J$. One of the most common examples is when we take our manifold to be $M=\mathbb{F}^{2n}$ and the symplectic form

$J=\begin{pmatrix}0&I_n\\-I_n&0\end{pmatrix}$

where $F$ is a field and $I_n$ is the identity matrix. This is a symplectic manifold, and the set of symplectic transformations is know as $Sp(n,F)$. This is a well known Lie Group acting by multiplication on $M$, and one of its goodness is that this action is transitive, that is, for any non-zero $x,y\in M$, there is $S\in Sp(n,F)$ such that $y=Sx$.

This statement was actually part of our homework, to prove that the action is transitive, and I wanted to find a nicer way to prove it and not to do a proof that I had seen before in my previous courses, so I started thinking a bit of many different ways of saying that this action was transitive.

One way of seen this is by turning around the problem saying what would happen if we let $S$ to run over $Sp(n,F)$ and look at $Sx$ for $x$ fixed? Well, that is saying something like the orbit of $x$ is $M/\{0\}$ and that started to sound a bit familiar.

I was trying then to use some kind of orbit-stabilizer theorem and then use some cardinality argument and kill the problem. Although, I only did remember the finite version of this powerful theorem, which obviously, wouldn't help me at all, but in essence, that was what I was looking for. A cardinality argument would not help me in this situation, because I could have some proper subspace of the same cardinality of $M$ and this wouldn't lead me to the conclusion I was going after. Instead, a dimensionality argument was needed.

While searching for this and thinking what actually was going on behind the scenes in this group action, I saw how helpful is the notion of representation for understanding a strange object.

If $G$ is a Lie Group, we call a representation of it, a vector space $V$ in which $G$ acts on. We can think as $G$ be some sort of subgroup of $Gl(V)$, the set of linear transformations of $V$ into itself. For an element $x$ of $V$, we can talk about the $G$ orbit through $x$, $O_x$ as the set of all $g.x$ for $g\in G$. In some sense, $O_x$ is a copy of the shape of $G$. Also, from the geometrical point of view, a Lie Group is a manifold, endowed with superpowers (group structure) and hence, we can think of these orbits into $V$ as coordinate maps of $G$ given by $\phi(g)=g.x$, so really $O_x$ is how $G$ looks locally.

For example, take $O(2)$, which is the group of all $2\times 2$ matrices $O$ such that $OO^T=I$. This group is quite odd to picture, since it is a 1 dimensional manifold living in a 4 dimensional space, but by means of orbits, one can have a pretty good idea of how this group looks like. By picking a nonzero vector $x$ and looking at its orbit in $\mathbb{R}^2$, one can find that $O(2)$ looks locally like a circle.

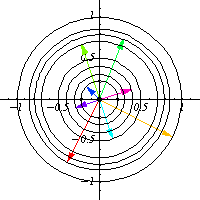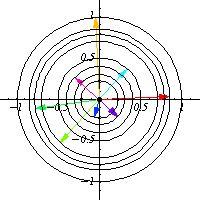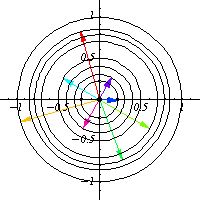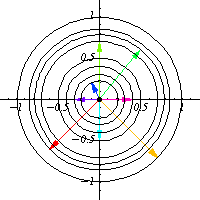
In the general case, one can think as $G$ being a covering for $O_x$ and the degree of the cover is the number of connected components of $G$, for instance, in the above case, $O(2)$ has 2 connected components, the set of matrices with determinant equal to 1 and those of determinant equal to -1, and that fact is reflected in $O_x$ as the vector $g.x$ rotates counter clockwise for $O(2)_e$ (the identity component) and rotates clockwise in the other component, so each circle is drawn twice, and that means that $O(2)$ is a 2-fold cover for each $O_x$.

In this language, we can say that the stabilizer $G_X$ of an element $x$, is the fiber $\phi^{-1}(x)$ whose cardinality gives us the degree of the covering map.

Actually, from this point of view, $\phi$ defines a quotient map, which is very suitable for an orbit-stabilizer type argument. Since the stabilizer $G_x$ is a normal subgroup, one can think of $G$ as a principal $G_x$-bundle as $G/G_x\times G_x$ and making the identification $G/G_x\sim O_x$ and $G_x\sim \phi^{-1}(x)$ we have that $G\sim O_x\times\phi^{-1}(x)$.

Going away from counting arguments and going more into dimensionality, I found the so called Orbit-Stabilizer Theorem for Lie Groups which have the same feeling as the covering map approach. It states that

$dim(G)=dim(O_x)+dim(G_s)$

where $dim$ is regarded as manifolds.

In the $O(2)$ case, we have that $dim(G)=1$, $dim(O_x)=1$ and $dim(G_x)=0$ as any of the other cases when $G_x$ is a finite group, and hence, we have that $\phi$ is a quotient map and $dim(G)=dim(O_x)$ as expected from a covering map.

At the end, I didn't use any of these arguments for my proof, but I found quite enjoyable doing this diversion from my first thought.

Tempo Musical y Espacios de Hilbert

Hoy durante el recital de piano de mi amigo Alfredo notaba algo extraño que desde mucho tiempo me ha acosado pero nunca habia puesto tiempo en analizar detenidamente, y es la increible capacidad que tiene el cerebro humano de comprender la música.

Notaba como de forma natural, lograba identificar el tempo en el que mi amigo interpretaba el piano, es decir, llevar el tiempo de la canción con mi pié, o como decimos coloquialmente, llevaba el ritmo.

Esto puede sonar una tarea muy sencilla de identificar, puesto que una forma tentadora de hacerlo es simplemente seguir el tiempo de las notas consecutivas, sin embargo, de esta forma se tendría un tempo errático, no regular en el tiempo. Parecería entonces que es cuestión de hallar un máximo común divisor entre estas separaciones de notas, pero de nuevo, esto no resuelve el problema de manera eficaz, pues en la mayoría de casos, se obtienen valores muy altos de bpm (beats per minute). Un valor típico de tempo esta cerca de los 120 bpm o 2 notas por segundo.

Luego de estos pequeños inconvenientes, me puse a pensar un poco en otro que es un poco mas sutíl, y es que si una canción está en un tempo $\tau$, matemáticamente es correcto tambien clasificarla con un tempo de $2^n\tau$, con $n\in\mathbb{Z}$, sin embargo, solamente una de estas opciones suena acorde en el cerebro.

Una cosa interesante es el factor de una potencia de 2 en los tempos equivalentes, aunque resulte muy natural dividir en 2 o duplicar el tempo, ¿porqué 2 y no otro número? ¿digamos 3?, ¿5?, ¿$\pi$? La respuesta quizás ya la haya abordado anteriormente, solo que en otra escala de tiempo. Si una nota suena igual una octava abajo o una octava arriba, naturalmente un tempo sonará bien si se duplica o se divide por la mitad. Ahora la pregunta es ¿cómo sabe nuestro oído cual es el factor correcto?

Una idea para abordar esta incógnita es representar una canción $\phi(t)$ por un vector en el espacio $M=\otimes_{\alpha\in\mathbb{R}}\mathbb{R}v_\alpha$, donde $v_\alpha$ es un vector de la base. Es importane notar que por definición diremos que los $v_\alpha$ son linealmente independientes, sin embargo podemos interpretar a $v_\alpha$ como $e^{\alpha t}$, es decir, los $v_\alpha$ viven en diferentes espacios de factores. Con esto tenemos que

$\phi(t)=\sum_{\alpha\in\mathbb{R}} c_\alpha(t)v_\alpha$

donde la suma es una serie formal y los $c_\alpha(t)$ no son otra cosa que los coeficientes de fourier de $\phi(t)$.

Como el tempo lo determina la cantidad de notas que se ejecuten, podríamos decir que está relacionado con las variaciones en la amplitud de los sonidos (prescencia o ausencia), en otras palabras, se podría analizar el comportamiento de $d\phi(t)$ en $M$, es decir

$d\phi (t)=\sum_{\alpha\in\mathbb{R}} d c_\alpha (t) v_{\alpha}$

esta fue la razón por la que resulta conveniente tomar los $v_\alpha$ como objetos abstractos, así al tomar la derivada no tenemos factores proporcionales a la frecuencia de cada armónica.

Ahora bien, la magnitud de este vector derivada puede darnos una idea de cuanto cambia el vector inicial $\phi$, por lo tanto podemos analizar en un intervalo de tiempo

$|d\phi(t)|^2=\int_a^b\int_{-\infty}^\infty|dc_\alpha(t)|d\alpha dt$

y tratar de relacionarlo de alguna manera con algo que nos mida el tempo en este intervalo. La integral interior converge puesto que dado que los coeficientes $c_\alpha$ son coeficientes de fourier, tenemos que $\phi$ es una función de potencia finita, es decir, una función en $L^2$ y por lo tanto $d\phi$ tambien sera de potencia finita.

El motivo de analizar el comportamiento de la señal en un intervalo es que el tempo de una canción es una cantidad que puede o no ser constante a lo largo de toda la canción, es muy frecuente que dependiendo del género musical, el tempo en efecto no sea un parámetro constante a lo largo de la canción, como es el caso del progresivo. Por lo tanto, podemos considerar el tempo como una propiedad semilocal y no una propiedad global, es decir, una propiedad que esta ligada a la longitud del intervalo sobre el cual se está analizando la canción. Para esto podemos analizar la senñal en un intervalo $[a,b]$, donde $(b-a)>>1/f_b$ donde $f_b$ es frecuencia de corte de bandabase de la canción, la cual está alrededor de los $8KHz$.

Una interpretación que podemos dar al tempo como el período de un tren de pulsos tal que al muestrear la canción original, es posible aún percibir el contenido de la canción. Con esto no me refiero a recuperar la señal original como en el caso del teorema de Nyquist, sino que a lograr identificar la melodia o el contenido musical de la canción.

Si denotamos por $\Delta_{\tau}(t)$ un tren de implusos unitarios con período $\tau$, la señal muestreada está dada por

$\Delta_{\tau}(t)*|d\phi(t)|^2.$

Podemos interpretar que el tempo es el valor ${\tau}$ que resuelve un problema de optimización actuando sobre la función anterior. El cerebro es un especialista en resolver problemas de optimización, como la visión bifocal de los ojos, que maximiza la cantidad de información obtenida por ambos ojos a la vez, o el sistema retroalimentado boca-oídos-ojos que minimiza el volumen de la voz necesario para transmitir un mensaje a otra persona. Por esta razón, suena a que este es otro problema en donde una optimización es llevada acabo.

Ahora bien, debido a la propia esctructura interna del oído, resulta más natural analizar esta función en el dominio de la frecuencia, ya que nuestros oídos son receptivos a los cambios en frecuencia y no a los cambios en el tiempo. Puesto que $|\phi'(t)|^2\in L^2(\mathbb{R})$, podemos estudiar su transformada de Fourier

$T(f)=\left( \sum_{n=-\infty}^{\infty} e^{-2\pi i n f \tau}\right)\widehat{|d\phi(t)|^2}$

Esta función es una función en $L^2$, por lo que podemos calcular su norma, la cual daría la cantidad de energía que posee, así que como lo establecimos antes, nuestro problema a minimizar puede ser el de encontrar $\tau_0\neq 0$ tal que

$\left. \frac{d ||T||_2}{d\tau}\right|_{\tau_0}=0$

en donde $\tau_0$ es un candidato al tempo de la canción. En la prática este problema de minimización puede ser resuelto solo mediante métodos numéricos, debido a los factores $e^\tau$ que se hallan en la función $\tau$. La verdad, no soy muy numero-analítico, asi que pequé de conformista y dejé el análisis hasta aca, pero sería una buena idea el tratar de implementar el algoritmo y analizar resultados experimentales.