Orbit-Stabilizer and Covering Maps

Last week, in our quantum Mechanics class, we were going over symplectic spaces and symplectic transformations. A symplectic space is just a manifold together with a skew-symmetric non-degenerate bilinear form $J$ defined on it, and a symplectic transformation $S$ is a transformation of the manifold into itself such that it preserves $J$. One of the most common examples is when we take our manifold to be $M=\mathbb{F}^{2n}$ and the symplectic form

$J=\begin{pmatrix}0&I_n\\-I_n&0\end{pmatrix}$

where $F$ is a field and $I_n$ is the identity matrix. This is a symplectic manifold, and the set of symplectic transformations is know as $Sp(n,F)$. This is a well known Lie Group acting by multiplication on $M$, and one of its goodness is that this action is transitive, that is, for any non-zero $x,y\in M$, there is $S\in Sp(n,F)$ such that $y=Sx$.

This statement was actually part of our homework, to prove that the action is transitive, and I wanted to find a nicer way to prove it and not to do a proof that I had seen before in my previous courses, so I started thinking a bit of many different ways of saying that this action was transitive.

One way of seen this is by turning around the problem saying what would happen if we let $S$ to run over $Sp(n,F)$ and look at $Sx$ for $x$ fixed? Well, that is saying something like the orbit of $x$ is $M/\{0\}$ and that started to sound a bit familiar.

I was trying then to use some kind of orbit-stabilizer theorem and then use some cardinality argument and kill the problem. Although, I only did remember the finite version of this powerful theorem, which obviously, wouldn't help me at all, but in essence, that was what I was looking for. A cardinality argument would not help me in this situation, because I could have some proper subspace of the same cardinality of $M$ and this wouldn't lead me to the conclusion I was going after. Instead, a dimensionality argument was needed.

While searching for this and thinking what actually was going on behind the scenes in this group action, I saw how helpful is the notion of representation for understanding a strange object.

If $G$ is a Lie Group, we call a representation of it, a vector space $V$ in which $G$ acts on. We can think as $G$ be some sort of subgroup of $Gl(V)$, the set of linear transformations of $V$ into itself. For an element $x$ of $V$, we can talk about the $G$ orbit through $x$, $O_x$ as the set of all $g.x$ for $g\in G$. In some sense, $O_x$ is a copy of the shape of $G$. Also, from the geometrical point of view, a Lie Group is a manifold, endowed with superpowers (group structure) and hence, we can think of these orbits into $V$ as coordinate maps of $G$ given by $\phi(g)=g.x$, so really $O_x$ is how $G$ looks locally.

For example, take $O(2)$, which is the group of all $2\times 2$ matrices $O$ such that $OO^T=I$. This group is quite odd to picture, since it is a 1 dimensional manifold living in a 4 dimensional space, but by means of orbits, one can have a pretty good idea of how this group looks like. By picking a nonzero vector $x$ and looking at its orbit in $\mathbb{R}^2$, one can find that $O(2)$ looks locally like a circle.

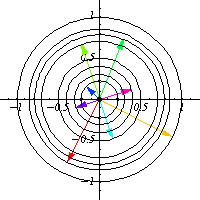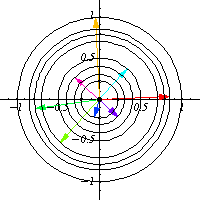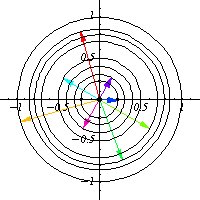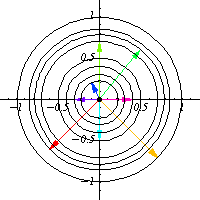
In the general case, one can think as $G$ being a covering for $O_x$ and the degree of the cover is the number of connected components of $G$, for instance, in the above case, $O(2)$ has 2 connected components, the set of matrices with determinant equal to 1 and those of determinant equal to -1, and that fact is reflected in $O_x$ as the vector $g.x$ rotates counter clockwise for $O(2)_e$ (the identity component) and rotates clockwise in the other component, so each circle is drawn twice, and that means that $O(2)$ is a 2-fold cover for each $O_x$.

In this language, we can say that the stabilizer $G_X$ of an element $x$, is the fiber $\phi^{-1}(x)$ whose cardinality gives us the degree of the covering map.

Actually, from this point of view, $\phi$ defines a quotient map, which is very suitable for an orbit-stabilizer type argument. Since the stabilizer $G_x$ is a normal subgroup, one can think of $G$ as a principal $G_x$-bundle as $G/G_x\times G_x$ and making the identification $G/G_x\sim O_x$ and $G_x\sim \phi^{-1}(x)$ we have that $G\sim O_x\times\phi^{-1}(x)$.

Going away from counting arguments and going more into dimensionality, I found the so called Orbit-Stabilizer Theorem for Lie Groups which have the same feeling as the covering map approach. It states that

$dim(G)=dim(O_x)+dim(G_s)$

where $dim$ is regarded as manifolds.

In the $O(2)$ case, we have that $dim(G)=1$, $dim(O_x)=1$ and $dim(G_x)=0$ as any of the other cases when $G_x$ is a finite group, and hence, we have that $\phi$ is a quotient map and $dim(G)=dim(O_x)$ as expected from a covering map.

At the end, I didn't use any of these arguments for my proof, but I found quite enjoyable doing this diversion from my first thought.