Acciones y el Teorema de Noether

Este semestre estoy tomando una clase de teoría de invariantes. Básicamente la clase trata de estudiar los espacios invariantes resultantes de una acción de un grupo sobre un espacio vectorial y de analizar la descomposición de las órbitas en subespacios invariantes. Es un tema muy interesante y divertido de estudiar. 

Unos de los invariantes más famosos ocurren en el estudio del álgebra lineal. Que la traza y el determinante de una matriz permanecen igual bajo cambios de bases son resultados que provocan el deleite de chicos y grandes. Acá lo que se hace es que se estudia el espacio $M_n$ de las matrices $n\times n$, digamos, sobre el campo de números complejos, luego se ve la acción del grupo $U(n)$ sobre $M_n$ por medio de

$g.A\mapsto g^{-1} A g$

y se analizan los invariantes de la acción. 

Ya que $\det$ es un homomorfismo de anillos entre matrices y números complejos, tenemos que el determinante de una matriz es preservado por la acción:

$\det(A)=\det (g.A)$

y de acá podemos ver que el polinomio característico de $A$ es otro invariante de la acción. Con esto, los coeficientes del polinomio característico también son conservados por el cambio de base, y según las formulas de Vieta, dichos coeficientes son simplemente las funciones simétricas elementales de los valores propios de la matriz $A$, siendo el término constante el determinante de la matriz y el término de grado $n-1$ la traza de la matriz. 

Luego de analizar un poco esta situación, nos damos cuenta que la única información relevante de una matriz $A$  para esta acción son los valores propios de la misma. En cierto sentido esta es la información que se conserva al efectuar la acción. 

De una manera similar, al considerar la acción de $SL(n)$ sobre $M_n$ por 

$g.A\mapsto gA$

se tiene que la cantidad conservada por esta acción es $\det(A)$. 

Este fenómeno es un poco más conocido en el ámbito físico. Es muy sabido que dentro de un sistema, las simetrías corresponden con cantidades conservadas. Quizás esto sea un poco más familiar al ser referido por su nombre artístico, el Teorema de Noether. Muchos hemos visto la prueba de este teorema, la cual quizás es un bonito ejercicio de calculo multivariado, en donde se utiliza el concepto de simetría para encontrar que la el cambio de una cantidad del sistema es 0. 

Una simetría de un sistema no es más que un invariante proveniente de la acción de un grupo. 

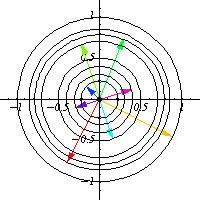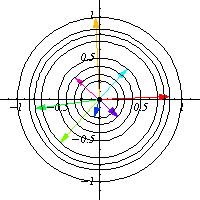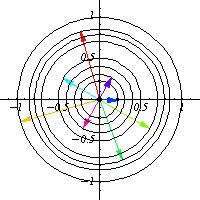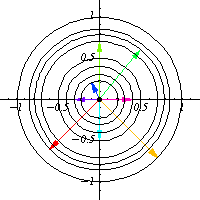
Por ejemplo, en la animación la acción es rotación (multiplicación por un complejo unitario) y la cantidad conservada es la norma del número complejo. En otras palabras, al ver las órbitas de la acción del grupo se obtienen las cantidades conservadas por dicha acción. Es importante el notar que las órbitas proveen una forma de visualizar el grupo que actúa sobre el espacio vectorial, por ejemplo en la anterior animación es posible ver que la forma del grupo que actúa es un circulo (complejos unitarios). Por esta razón es que el estudio de las acciones de grupos recibe el nombre de teoría de la representación, puesto que al ver las acción del grupo se ve indirectamente la forma del grupo en sí. 

La idea es que una acción de un grupo puede relacionarse con una acción local de su álgebra de Lie sobre el espacio tangente, o equivalentemente, la derivada de la acción puede verse como una especie de campo vectorial definido sobre el espacio vectorial. El espíritu del teorema de Noether es que, al igual que pasa en calculo multivariado, la integral cerrada sobre cualquier superficie de un campo conservativo siempre da 0, es decir se tiene una conservación del flujo del campo vectorial. 

Es posible pensar que la acción de un grupo produce de alguna manera un campo conservativo puesto que en la mayoría de los casos las acciones son bien portadas, es decir, son suaves. El problema con campos conservativos es que tienen singularidades, cosa que no pasa con una acción bien portada. 

Al ser el flujo conservado dentro de una superficie cerrada, esto da que la cantidad de masa dentro de la superficie es una cantidad conservada. 

Lo interesante es ver que cada vez que se tiene una acción sobre un espacio vectorial se pueden encontrar cantidades conservadas, aunque el encontrar dichas cantidades algunas veces es una tarea un poco difícil. 

Invariant polynomials and geometric transformations

A couple days ago, I stumbled over a really interesting problem looking for something to post for #ProblemOfToday. It was a problem that appeared in the 1989 Putman exam and reads as follows

"Prove that if 

$11z^{10}+10 i z^9 + 10 i z -11 =0$

then $|z|=1$."

It is a really nice problem in itself, but after thinking a bit on it, I thought what was so special about this specific coefficients to have this nice property. First, the polynomial can be analyzed in an even nicer way. By doing the transformation $z\mapsto i z$ we can see that the polynomial gets mapped (up to a negative sign) to:

$11z^{10}+10z^9+10z+11$

In this form one can see better how is the dependence of the polynomial on one of the coefficients (say 10), and can quickly ask a generalization of this particular problem:

If 

$(n+1)z^n+nz^{n-1}+n z+ (n+1)=0$

then $|z|=1$ for $n\in\mathbb{Z}/\{0\}$.

Doing a couple of special cases, one can get convinced that actually the previous statement holds true. 

$n=-4$ 

$n=10$

In the general case maybe the answer relies in a geometric argument. The polynomials $p_n(z)=(n+1)z^n+nz^{n-1}+n z+ (n+1)$ have the peculiarity that their roots are invariant under the  inversion of the complex plane, i.e. by doing the transformation $z \mapsto \frac{1}{z}$, we have that

$p_n(z)=z^np_n\left(\frac{1}{z}\right)$

that is, roots are mapped into roots by the inversion. 

Therefore, if there is a root bigger than 1, there should be a root smaller than 1 and vice-versa. It is not difficult to see that here cannot be a root bigger than 1, as $(n+1)z^n+nz^{n-1}$ and $n z+ (n+1)$ would have to be equal in modulus, but their orders of magnitude are different. 

Another way of proving this is by analyzing $p_n\left( e^{i \theta}\right)$. After a little simplification we have that $p_n\left( e^{i \theta}\right)=2e^{\frac{i \theta n}{2}}\left( n\cos\left( \frac{(n-2)\theta}{2}\right)+(n+1)\cos\left( \frac{n\theta}{2}\right)\right)$, which can be found to have exactly $n$ real roots for $\theta$. Hence all roots of $p_n$ lie on the unit circle.

The interesting fact is that for $n\to\pm\infty$, the roots of $p_n(z)$ become dense on $S^1$

For example, the graph of the absolute value of $p_21(z)$ is given by

where the $S^1$ can be seen. Likewise, for negative values of $n$ we can recover $S^1$

It looks like the $p_n(z)$ can be thought as some orthogonal polynomials whose support is $S^1$, and for the same reason, it is also natural to think that they can be eigenfunctions (up to a renormalization) of some operator (hopefully differential!).

Viernes 13

Como si no fuera poco con toda la propaganda sobre el fin del mundo, este 2012 comienza con otro indicio de mala suerte, hoy es viernes 13.

Tradicionalmente el viernes 13 ha sido catalogado como un día de mala suerte en muchas culturas del mundo, aunque posee una mayor influencia en la cultura anglosajona. En latinoamérica también es acostumbrado atribuirle malos augurios al martes 13, aunque ultimamente ha perdido seguidores quizás por la gran influencia cultural que el sistema anglo tiene sobre el resto del continente. También es curioso que en ambos casos la fecha es un número primo, aunque quizás tenga más relación con el hecho de que 13=12+1 (algo parecido pasa con el 6 y el 7).

Recuerdo que hace unos años atrás, en una clase de entrenamientos de olimpiadas surgió el tema del viernes 13. Estabamos recibiendo clase de probabilidades y nuestro profesor nos hizo el comentario acerca de que tan probable era en realidad que hubiera un viernes 13.

Si vemos tan solo la probabilidad de que el dia 13 de un mes sea viernes, estaríamos tentados a decir que dicha probabilidad es $1/7$, puesto que hay 7 posibles días de la semana (lunes, martes, etc.). Sin embargo el día de la semana y la fecha no son eventos completamente independientes, por lo tanto nuestro $1/7$ no es del todo correcto.

Para poder calcular la probabilidad correcta, es necesario contar cuantas veces un viernes 13 puede ocurrir. Para esto notamos que un mes tendrá un viernes 13 si dicho mes comienza en domingo. Este año 2012 habrán 3 viernes 13, en enero, en abril y en julio. Ahora, para poder calcular la probabilidad de un viernes 13 hay que tener claro lo que significa calcular la probabilidad. La forma más elemental de hacer esto es dividir el número de casos buscados sobre el número de casos totales, y para esto necesitamos saber que se entiende por casos totales en este contexto. Si el universo sobre el cual calculamos nuestra probabilidad es el número de viernes que hay en un año, tendríamos que nuestra probabilidad es $3/52$, ya que este año habrán 52 días viernes en total. Si por otro lado nuestro universo es el número de días 13, la probabilidad sería $3/12$, así que la pregunta central es ¿qué significa la probabilidad de un viernes 13? ¿Queremos calcular la probabilidad que un viernes sea 13? o ¿la probabilidad que un día 13 sea viernes? o ¿la probabilidad que un día sea viernes y sea 13? Creo que la ultima pregunta es la que describe mejor lo que andamos buscando, por lo tanto para el año 2012 tendríamos que la probabilidad es $3/366$.

El caso de 2012 es un caso especial, dado que es un año bisiesto, pero en general para calcular la probabilidad de que haya un viernes 13, es necesario analizar más detenidamente el calendario gregoriano. Al principio parecería suficiente ver dos casos, cuando el año es bisiesto y cuando no, sin embargo el calendario gregoriano es un poco más elaborado y un análisis un tanto más riguroso es necesario. 

Nuestro calendario tiene un período de 400 años, es decir, cada 400 años se repite exactamente el calendario, por ejemplo el 2412 comenzará en un domingo y habrán exactamente 3 viernes 13. Por lo tanto, contando el número de viernes 13 en un período de 400 años y dividiendo esto dentro del número total de días dará la probabilidad exacta de que haya un viernes 13.

Calculando este número (ya sea viendo un calendario, escribiendo un programa en excel o buscando en internet) da un total de 688 veces, así que dicha probabilidad es

$\frac{668}{149067}\sim 0.004481206437373798359127103919714$

Lo cuál es una probabilidad muy pequeña, sin embargo no es tan pequeña como para ser considerada de mala suerte. De hecho la mayoría de días 13 son viernes, por ejemplo, este año habrán 1 domingo, 2 lunes,

2 martes, 1 miércoles, 2 jueves, 3 viernes y 1 sábado que caerán días 13. Haciendo la misma cuenta sobre un período de 400 años es posible ver la distribución de días 13 en la semana. Tenemos que hay un total de 687 domingos, 685 lunes, 685, martes, 687 miércoles, 684 jueves, 688 viernes y 684 sábados que caen día 13, así que los viernes 13 son de hecho los días que más abundan, siendo los jueves 13 los menos frecuentes.